The
mystery
Spontaneous
radioactive decay
The double slit experiment
Quantum entanglement
What does it mean?
A
few additional web links
Some time after Einstein's General Theory of Relativity was published, Arthur Eddington is said to have been asked if it was true that only three people in the world understood the theory. Sir Eddington thought for a moment and said: "Who would that third person be?"
 |
|
For Physics World by John Richardson |
The situation is even worse with regard to Quantum Mechanics. Richard Feynman, who received the Nobel prize in 1965 "for his fundamental work in quantum electrodynamics, with deep-ploughing consequences for the physics of elementary particles" had this to say: "I think that I can safely say that nobody understands quantum mechanics."
The basic theory was developed in the late 1920s. It was subsequently refined to the point where it is now the most successful, thoroughly tested, and precise theory we have ever had with which to explain and predict physical phenomena. It is routinely used by thousands of scientists and engineers on a daily basis and has found widespread practical use. - Yet even after two thirds of a century, its concepts and predictions are so baffling and at odds with our intuition and common sense, that a hot debate is still raging over what it really means.
Can something be said to exist if it cannot be observed even in principle? Can a physical object be in several places at once? Can there be an effect without a cause? Can measurements on a physical system influence a physical system that is far removed from the first system instantaneously (not at the speed of light - instantaneously!)?
Let us consider three puzzling phenomena: spontaneous radioactive decay, the double slit experiment, and quantum entanglement.
More than a hundred years after Becquerel discovered radioactivity
in uranium crystals, we still are unable to predict when an individual
radioactive atom will decay.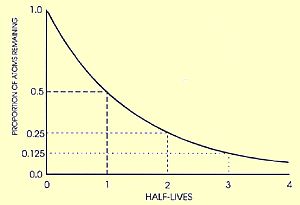 
Most
isotopes of the 92 basic elements in nature (and all man-made elements
with higher atomic numbers) spontaneously decay into other elements.
This occurs with a half-life (i. e. the time it takes for half of the
original sample to decay) that varies widely between different isotopes,
but is quite well-defined for each particular isotope. -
Carbon 14, commonly used in the dating of human remains and artefacts,
has a half-life of 5730 years. Iodine 131 has 8 days, Uranium 238 well
over 4 billion years, Polonium 212 just 300 nanoseconds.
This decay occurs according to a stringent physical law: an exponential decrease of the original sample at a rate that is specific to each isotope. It is not affected, as far as we know, by the external environment (temperature, pressure etc). But it is a statistical law. We can make no prediction concerning an individual atom, just determine the probability that it will decay during a given time interval.
Two different explanations have been given for our inability to predict the fate of the individual atom:
- We simply do not know enough about the inner workings of the atom.
The atoms of a particular isotope may not be identical to each other.
Perhaps there is an interior structure, of which we have no knowledge,
that determines how stable the individual atom is.
This is the "hidden-parameter" scenario. It comes in two flavors: a) We may in time come to develop our understanding to the point where we can make predictions, at least in principle, for the decay of individual atoms. b) There is an inner structure that differentiates one atom from the next and determines exactly when it will decay, but it will remain hidden from us forever because of fundamental limits to observability.
- Each atom of the same isotope is identical. Its structure determines its half-time, which can be measured and may be accessible to calculation. The decay of the individual atom, on the other hand, is an intrinsically random event governed by its probability, and there is no additional law to discover.
The second standpoint has been the prevailing view among leading scientists for the better part of a century; with some notable exceptions, including Einstein. ("I cannot believe that the good Lord is playing dice with the universe.") But even Einstein admitted that a probabilistic universe was not a logical impossibility.
Intuitively, it seems hard to accept, though. "How does an atom know when to decay?" After all, probability theory has been developed as a discipline to describe deterministic phenomena that are too complex to analyse in detail (the toss of dice, morbidity, atmospheric turbulence...). It seems quite a stretch to believe that the universe is intrinsically probabilistic. And if an atom can undergo a transition without any external triggering event, what about the universe itself?
On the other hand, suppose that all atoms of a certain isotope really are identical (except for external attributes such as position), then, in a deterministic universe, we would expect them all to exhibit the same behavior. If their stability (or lack thereof) is such that it corresponds to a median life of 5730 years, we would expect them all to decay simultaneously after an interval of that order of magnitude. Poff! - Such a scenario seems just as difficult to envision. Yet, after a century of increasingly refined measurements, including the discovery of many subatomic particles and the modelling of quarks, no evidence has ever been found for any kind of individuality at the atomic level.
|
Nature
and Nature's laws lay hid in night: God said, "Let Newton be!"
and all was light. - Alexander Pope
|
|
It
did not last: the Devil howling "Ho! Let Einstein be!" restored
the status quo. - J.C. Squire
|
For centuries, there were divided opinions on the nature of light. Around 1700, Huygens held that light was a wave phenomenon, while Newton thought that light consisted of tiny corpuscles. A hundred years later, the wave theory got the upper hand, when interference was discovered, and the double slit experiment (see below) was first performed by Thomas Young. Later in the 19th century, visible light was identified as electromagnetic radiation within a certain wavelength band, and was shown to be governed by Maxwell's equations. The case seemed settled.
Ironically, it was Einstein who unwittingly opened the door to quantum mechanics and all its paradoxes by proposing that light itself was quantized into what came to be known as "photons". This explained the photoelectric effect and won him the physics Nobel prize in 1921 (thereby letting the Swedish Academy of Sciences off the hook of having to take a stand on the still controversial Theory of Relativity). However, Einstein's discovery raised as many questions as it answered. In particular, the double slit experiment needed to be revisited.
 |
In this experiment, coherent light (coming from above in the illustration at right) illuminates two parallel narrow slits (having a width on the order of the wavelength of the light). Each of the slits will then act as a light source, and the screen at the bottom will exhibit an interference pattern with alternating lighter and darker bands. - This effect is strikingly similar to the pattern we would get if we threw two stones of similar size into a pond, with the two systems of waves alternately reinforcing and cancelling out each other in different spots. It clearly demonstrates the wave nature of light. It also seems to disprove the theory of light as small corpuscles travelling in straight lines. But the quantization of light had by now (in the 1920s) been firmly established. Somehow light seemed to exhibit some of the characteristics of both waves and particles. Scientists started to talk about "wave packets".
As early as 1909 it was discovered that the interference pattern in the double slit experiment persisted even when the intensity of the light source was drastically reduced. This later led to Dirac's famous exclamation: "The photon interferes with itself!" - Around 1930 it was shown through experiments involving diffraction off crystals that electrons, too, exhibit wavelike characteristics. (Double slit experiments with single electrons were not actually performed until the 1960s. They confirmed that electrons behave exactly in accordance with quantum theory, as expected).
The baffling fact, which had been firmly established around 1930, was
this: If electrons were sprayed at the two slits in the diagram, an
interference pattern similar to the one for light would occur on the
screen at the bottom. This was absolutely in contradiction to classical
physics, where the electrons would be expected to be grouped behind
the slits without any interference fringes. Moreover, this interference
pattern could be observed even if the electrons were fired one at
a time, but only if no attempt was made to measure which slit the
electron was passing through. This meant that each electron was indeed
interfering with itself! Somehow each electron was simultaneously
passing through both slits! But if measurements were made to determine
the path taken by the electron, the interference pattern vanished! So
the electron went through both slits at the same time only if no one
was looking!
 |
|
Cartoon
by Nick Kim.
|
These and other observations led to the formulation of quantum theory through legendary scientists such as Planck, Bohr, Schrödinger, Heisenberg, Dirac, de Broglie, Pauli and others. At its heart is the concept of uncertainty. It is fundamentally impossible to simultaneously measure the exact position and the exact momentum of a particle. The same goes for its exact energy at an exact point in time.
These limits to observations are due to the fact that all observations involve a disturbance of the observed entity of at least one quantum of energy. In the microscopic world this is enough to influence the observed system, so that it is fundamentally impossible to disentangle the observer from the observed object.
Mathematically, particles are described by a wave function denoted with the greek letter psi. This is a highly abstract entity. In the opinion of many scientists it is devoid of physical meaning, but it allows the calculation of physically relevant parameters. For instance, the square of the absolute value of psi at a certain point in space is proportional to the probability of detecting the particle at that point, if a measurement is made. Particles such as electrons or photons are envisioned as tiny smeared-out clouds, where the central parts correspond to their most probable locations.
In the double slit experiment, when a particle is fired, there is a 50 percent chance that it will pass through the left slit, and an equal probability that it will pass through the right slit, assuming symmetry. This is reflected in the psi function which becomes a superposition of the two states corresponding to passage through one slit or the other. When the particle hits the screen at the far side, the psi function will predict bands of probability for the postion of the particle that correspond exactly to the fringes observed. If a measurement is made to determine through which slit the particle actually passes, the wave function "collapses" and is no longer a superposition of two states, and the interference fringes vanish.
In the more than seventy years since quantum mechanics was invented (or discovered, take your pick), it has withstood every test. Its predictions of the outcome of experiments are invariably exactly fulfilled. But it still leaves open the question: What does it really mean?
According to Niels Bohr, physical reality is that which can be observed. Atoms and particles are real, but the psi function has only symbolic meaning and does not represent anything real. It is not only pointless but also meaningless to speculate about the reality of things we cannot observe. Such speculations lie outside the realm of science, for they cannot be put to the test of experiments. - This has come to be known as the Copenhagen interpretation and has dominated thinking among scientists since it was put forward.
Einstein is said to have countered: "Do you really think the
moon isn't there if you aren't looking at it?" Not only Einstein,
but also such a central figure as Schrödinger, who formulated the
fundamental equation for describing quantum mechanical behavior, was
uncomfortable with the role accorded to the observer in the Copenhagen
interpretation of the theory.
Schrödinger devised a thought experiment intended to show that the analysis of the role of observation in quantum mechanics was incomplete. A cat is placed in a sealed box for an hour together with a radioactive substance with the characteristic that there is exactly a 50 percent chance that an atom will decay during that hour. If an atom decays, it triggers the release of poison gas, killing "Schrödinger's cat". Now, according to quantum mechancis, in the absence of an observation, the cat exists as a superposition of two states just before we open the box: dead and alive. Only when we open the box and make the observation, the wave function "collapses" and the fate of the cat is decided. But this is manifestly absurd. The cat must be either alive or dead whether we are looking or not. If it turns out to be dead when we open the box, we can easily establish how long it has been dead.
If you find it surprising that a particle can simultaneously pass through two slits, just wait: it gets weirder. According to quantum theory, two particles that interact become entangled from that point on. They are both described by a single combined wave function. If a measurement is made on one particle, it instantly influences the state of the other particle no matter how far the two particles are separated from each other.
|
Nearly all the giants of physics were present at a series of conferences arranged by the Belgian industrialist Ernest Solvay, the very same Solvay who financed the Solvay hut on the Matterhorn! |
 |
|
Solvay conference 1911. I am particularly fond of this picture, as I have spent many hours staring at it in the main conference room at the Joint Research Centre in Ispra, Italy. |
|
Click
to enlarge and access mouse-over links.
|
 |
|
Solvay conference 1927. Its theme was "Photons and electrons". This meeting came at a key moment in the development of quantum theory. |
|
Click
to enlarge and access mouse-over links.
|
You might say: "Big deal! If someone puts a black marble in one box and a white marble in another box behind my back and sends one of the boxes to Mars, I can determine the color of that marble just by opening the box left behind. That does not mean that my 'measurement' influences the color of the marble on Mars." But this is not what the theory says. It actually states that the measurement of one entangled particle instantaneously affects the state of the other particle, and this has been experimentally verified. Moreover, it is close to being exploited in practical applications such as quantum computers and quantum cryptography.
"But I thought that no signal can travel faster than light", you might say. The answer to that, according to quantum theory, is that this "communication" between the particles does not involve any signal in the conventional sense and cannot be used to transmit information from one observer to another. But even if we accept this, it implies that to some observers the state of the second particle will be found to have been influenced by the measurement on the first particle before it occurred, according to the special theory of relativity!
Einstein was the first to point out that this non-locality was required by quantum theory. In a seminal paper in 1935, he and his students Rosen and Podolsky concluded that either quantum mechanics was incomplete and particles must have definite states even when they were not measured (hidden parameters), or action at a distance was necessary, which meant that in some frames of reference an effect could precede its cause. They argued that a particle must have a definite state even in the absence of an observer. Einstein rejected what he called "spooky action at a distance". (See also this web article.)
Three years earlier, the eminent mathematician John von Neumann had shown that hidden-parameter theories could not be consistent with observed reality. His proof ultimately turned out to be flawed, but for some time it seemed very persuasive. In 1952, David Bohm succeeded in doing "the impossible" (John Bell). He devised a consistent theory of quantum mechanics allowing "hidden parameters", i. e. a deterministic description where the observer lost his key role in defining reality (in the Copenhagen interpretation). The theory, which built on a similar model from the 1920s by Louis de Broglie, involved the concept of pilot waves guiding particles in such a manner that all the manifestations of wave-like and particle-like behavior were respected, while restoring the reality of particle trajectories between observations. The theory was shown to be mathematically equivalent to the standard theory of quantum mechanics. - Bohm's theory was widely criticized for violating Occam's razor by adding assumptions beyond what was necessary to explain observations, however. To some it was reminiscent of Ptolemy's invention of epicircles to predict planetary motion, when a simpler model (Kepler's laws) did a better job. Some scientists felt that Bohm's theory was an excursion into metaphysics. - It certainly was not part of the curriculum (textbook by F. Mandl.) when I studied quantum mechanics in the early 1960s.
Then in 1964, John Bell published his famous theorem, which in essence states: No physical theory of local hidden variables can ever reproduce all of the predictions of quantum mechanics. This seemed to strengthen the Copenhagen interpretation: the world is probabilistic. What was widely overlooked was the word "local". A deterministic universe was still possible, but then "spooky action at a distance" had to be accepted.
In 1982, experiments seemed to demonstrate conclusively that the predictions of quantum mechanics concerning entanglement are correct, while the predictions of "objective local" theory are wrong. Subsequent experiments have confirmed this result, except for a few cases where it is believed that errors were introduced in the experiment setup. More recently, quantum entanglement has been demonstrated at separation distances of greater than 10 km. Other effects dependent on quantum entanglement, such as quantum teleportation and quantum cryptography, have been demonstrated in the laboratory. Here is an article from 2001; and here is a news item from December 2005, reporting that six Beryllium ions have been coaxed into spinning in opposite directions at the same time.
At this point my head is in a (classical) spin. It is time to disentangle myself before quantum collapse occurs, so I refer to another source for a discussion of the implications for causality of quantum entanglement, which I anyway am too lazy to try to understand :-). And here is a fairly recent article, directed at the general public, outlining the contributions of the 2022 Nobel physics laureates "to investigate and control particles that are in entangled states" .
Our present standard theory of quantum mechanics has been extremely successful in modelling physical reality. All attempts to "falsify" it, i. e. to make observations which contradict theory, have failed. Thus, any future theory attempting to replace present theory will have to make the same predictions concerning the outcome of previously conducted experiments within the present accuracy of our measurements (just as the predictions of the special theory of relativity become indistinguishable from those of newtonian mechanics at low speeds).
This means that "spooky" effects such as those described earlier are real, however much they may offend our intuition and "common sense". The scientific debate is not about the reality of these effects, but about their interpretation. Many scientists feel uncomfortable with concepts such as indeterminacy, non-locality, and non-causality, and look for a more "rational" model that would explain the observations.
I have seen at least six interpretations of quantum theory on the Web, most of which attempt to replace the "positivistic" Copenhagen interpretation with something considered to be more palatable and/or understandable. Four of them appear to have the following characteristics:
1. The Copenhagen interpretation
Physical reality is by definition that which can be observed. To speculate
about what happens when "no one is looking" is outside the
realm of science. 
The
question of whether objects have reality when they cannot (even in principle)
be observed has no physical meaning.
Quantum mechanics is complete insofar as it can correctly predict the outcome of all experiments to which it is subjected. There is therefore (at present) no need for additional "laws" or assumptions.
Physical reality is inherently probabilistic.
2. Bohm's pilot wave interpretation
As mentioned above, this is mathematically identical to the standard model, but makes the assumption of waves guiding particles so that the latter exhibit wave-like behavior. It is deterministic (hidden parameters) but non-local, so instantaneous action at a distance is allowed.
3. The Many-Worlds interpretation
Every probabilistic event spawns a separate universe for every possible outcome of that event. Such problems as "How does a radioactive atom know when to decay?" are addressed by proposing that all possible outcomes are realized in a multitude of separate universes. Our universe is no more real than all the others. There are infinitely many alternative non-observable universes.
This interpretation may perhaps offer some comfort to those who have been the subject of an improbable accident: There are many more universes, just as real, where the accident did not happen!
4. Waves travelling backward in time
This "transactional" interpretation by John Cramer builds on ideas from Wheeler and Feynman on time-symmetric radiative processes (if I have understood correctly). An emitter sends a wave forward and backward in time. When the forward wave hits an absorber, a new set of forward and backward waves is generated. "The emitter can be considered to produce an 'offer' wave which travels to the absorber. The absorber then returns a 'confirmation' wave [backward through time] to the emitter and the transaction is completed with an 'handshake' across space-time." To an observer, a photon has been emitted and absorbed, but the model can just as well be interpreted to mean that a standing wave has been established between emitter and absorber.
Mathematically, this is just another interpretation of the existing formalism. It makes no predictions different from the Copenhagen interpretation, but Cramer claims that it helps develop intuitions and insights into quantum phenomena that up to now have remained mysterious.
All of these interpretations are equivalent, in the sense that they assume, or can be shown to generate, the same governing equations and predictions. They are all interpretations rather than theories, as they make no additional predictions that would make it possible to test their validity. In a sense, they are therefore no more helpful than a claim that "the Universe was created last Thursday with all its present features, including evidence and memories of a much longer history", which also cannot be disproved. But they may be of some value in helping scientists think about quantum theory, and in suggesting avenues for research.
Personally, I find it quite remarkable that not only laymen, but also philosophers and theologians, seem to take so little interest in the amazing discoveries made during the past century about the nature of physical reality. It appears that even educated people often just have vague notions about clocks slowing down near the speed of light, and about quantum uncertainty. It is common to hear people ask: "But what happened before the Big Bang?" without realizing that "before" has to do with time, and that time is a feature of our physical universe.
Another thought is that the crucial role of the observer in defining
physical reality in the Copenhagen interpretation, which seems especially
hard to swallow to many physicists who believe in an "objective"
reality, perhaps should not be dismissed out of hand. 
Consider
a universe completely devoid of life and even of complex molecules,
from its Big Bang, expanding forever and ending up as a cold empty void
when the very last subatomic event has taken place after, say, 10100
years. What exactly do we mean when we say that such a universe has
an "objective" existence?
According to Albert Einstein: "The most incomprehensible thing about the universe, is that it is comprehensible." - While it does not appear all that comprehensible to me, it certainly seems surprising that the laws of physics are as simple and straightforward as they are, even when they are at odds with our intuition. When you think about it: is it not surprising that there should be any laws of physics?
There are a huge amount of articles, web links and on-line lectures on quantum entanglement available on the Web. I feel that I have not been keeping up, so am settling for fixing some broken links without further recommendations.
- "Quantum Mysteries", a short survey by John Gribbin.
- A one-hour video lecture on "Quantum Entanglement: Weird but useful" by Sir Peter Knight, Imperial College at:
- History of Physics at http://www.aip.org/, including many "oral history" interviews.
- "Experimental loophole-free violation of a Bell inequality using entangled electron spins separated by 1.3 km", 2015 scientific paper.
Last
edited or checked February 26, 2024. Broken links fixed or replaced May
29, 2024.